The Stochastic Indicator -- A simple classic
There isn't much to this indicator, it's a classic. This version returns the raw, slow K%, and slow D% calculations.
Disclaimer: the following post is an organized representation of my research and project notes. It doesn’t represent any type of advice, financial or otherwise. Its purpose is to be informative and educational. Backtest results are based on historical data, not real-time data. There is no guarantee that these hypothetical results will continue in the future. Day trading is extremely risky, and I do not suggest running any of these strategies live.
As the caption hinted, there isn't much complexity to this indicator. The original Stochastic indicator was created by a fellow named George Lane.[1] Since then, it has been tweaked a few times, mostly with different types of simple smoothing. These days, most version of the indicator utilize a fast exponential smoothing over the original simple moving average used to smooth the results. In this discussion, we're diving into a version of the indicators that lets you pick between the raw (OG) stochastic, a once smoothed, or a twice smoothed value--whichever suits your needs best.
If I am being honest, this indicator was a bit easier to code than some of the previous ones. However, it led me down another rabbit hole of updates for the pqt library. The first update was to stop using Yahoo!Finance historical data and start using the Norgate Data (ND) that I've been paying for and using with RealTest. While I was looking at the ND SDK documentation, I came across a data format called "record arrays" or recarray.
I did a little digging, and what I found had me asking myself: Can I avoid using the Pandas library altogether? Would that speed up the indicator report functions? Would this be difficult? Do other data providers also provide their data in recarrays?
Testing this meant I had to make multiple minor changes across all of the report functions in the library. Luckily, none of the underlying calculation functionality needed to be updated--they already took in np.ndarray objects for calculation. The report functions took in Pandas DataFrames and then converted the data into arrays for calculation and looping. After testing this approach with the Stochastic indicator, I noticed a pretty decent speed increase, so I decided to go ahead and apply this treatment to the entire suite of reports.
So, none of the reports take DataFrames anymore--they now operate with record arrays and regular ol' arrays. It took five minutes and thirty seconds to test three indicators, each with over 7k cases of data each and with 1000 permutation tests over three different tests. This was an improvement of about four minutes over the previous version. Fuck yeah.
It's still slow, don't get me wrong. I'm impatient. I want that shit yesterday. Unfortunately, I'm not there yet. I'll keep chipping away at it as I learn. I know that Python has limitations, but I'm determined to push those boundaries as I figure things out. I'm sure that the treatment I gave the library this past week is not the best way to optimize it. I know there are more simple methods I can use to speed up these operations. As soon as I learn about them, I'll test them and make adjustments. Until then, five minutes isn't so bad for what we're getting with these tools.
Got any other news or updates for us, Larry?
I do, but I am not going to clutter this post with them. I'll drop an update post tomorrow. A strategy will drop this weekend too. Also, notice that this post isn't just for paid subscribers? Keep an eye out for the update post and I'll explain why.
Nice. What about a lesson from the past?
Nope.
The Stochastic Indicator
The original stochastic indicator was based on the observations that closing prices tended to be closer to the upper or lower end of price range during up/down trends.[1] I am going to refer to the raw stochastic as the fast K%, the once smoothed version as slow K%, and the twice smoothed as slow D%. This follows the naming conventions found in reference two. We calculate the raw stochastic with the following equation:[1][2]
where:
Close_t: Represents the closing price at time
min(low): Represents the lowest low over the lookback period from t minus lookback to t.
max(high): Represents the highest high over the lookback period from t minus lookback to t.
This formula calculates the Raw Stochastic value, where the high and low values are taken over the specified lookback period. In Python, this can be written with something like:
highest = np.max(high[-lookback:])
lowest = np.min(low[-lookback:])
raw_k_value = (close[-1] - lowest) / (highest - lowest + 1.e-60) * 100.0
CopyFast Exponential Smoothing
The first type of smoothing that was applied to the stochastic indicator was done with a simple smoothing average, but the modern variation uses a fast/simple exponential smoothing.[2] This exponential smoothing can be expressed with the following equation:
where:
St: Represents the smoothed value at time t.
Vt: Represents the original value at time t from the
valuesarray.a: The smoothing factor, which determines the weight of the current value in the smoothing process.
St-1: Represents the smoothed value at time t-1, i.e., the previous smoothed value.
The formula applies exponential smoothing, where:
The new smoothed value St is a weighted average of the current value Vt and the previous smoothed value St-1.
The factor a determines how much influence the current value Vt has on the smoothed value compared to the previous smoothed value St-1.
Code
The first function I want to code is the fast exponential function. It will be used inside of the stochastic function to calculate the possible smoother variations of the indicator. It is simple enough that we can code can use Numba's JIT decorator in "nopython" mode. The function will take in an array of values and return the smoothed array. You can optionally change the weight distribution in the smoothing if you like but the default is set at 0.33333333. It will loop through the array
@jit(nopyton=True)
def fast_exponential_smoothing(values, alpha=0.33333333):
"""
Apply exponential smoothing to an array of values using a loop with JIT.
:param values: numpy array of values to smooth
:param alpha: smoothing factor (default is 0.33333333)
:return: numpy array of smoothed values
"""
smoothed_values = np.zeros_like(values)
smoothed_values[0] = values[0] # Initialize the first value
for i in range(1, len(values)):
smoothed_values[i] = alpha * values[i] + (1 - alpha) * smoothed_values[i - 1]
return smoothed_valuesWe can test the speed of the function with something like this:
# Generate a large random array of a million integers
large_array = np.random.randint(1, 100, size=1_000_000)
# Test the speed of fast_exponential_smoothing
start_time = time.time()
smoothed_result = fast_exponential_smoothing(large_array)
end_time = time.time()
print(f"Exponential Smoothing with JIT took {end_time - start_time:.6f} seconds with 1,000,000 sample array.")On my machine I got these results:
Not too bad. Let's move on to the stochastic indicator.
This function will take in arrays for the high, low, and close prices of an instrument, the lookback length, the level of smoothing, and a Boolean for subtracting fifty from the final result. The raw stochastic calculation can be done in a simple loop, making this function another candidate for JIT-compilation.
Raw Stochastic Calculation:
raw_k_values = np.zeros(len(close) - lookback + 1)
# Create the array of raw stochastic values.
for i in range(lookback - 1, len(close)):
# Moving the raw_stochastic logic here
highest = np.max(high[i - lookback + 1:i + 1])
lowest = np.min(low[i - lookback + 1:i + 1])
raw_k_values[i - lookback + 1] = (close[i] - lowest) / (highest - lowest + 1.e-60) * 100.0The next portion of code deals with the exponential smoothing. Zero returns the raw stochastic value discussed above, one returns the once smoothed values, and two returns them twice smoothed. If any other parameters are given it results in an error.
if n_smooth == 0:
stochastic_values = raw_k_values
elif n_smooth == 1:
stochastic_values = fast_exponential_smoothing(raw_k_values)
elif n_smooth == 2:
first_smooth = fast_exponential_smoothing(raw_k_values)
stochastic_values = fast_exponential_smoothing(first_smooth)
else:
raise ValueError("n_smooth must be 0, 1, or 2.")The next section addressed the sub50 parameter, which just determines if you want the values subtracted by fifty so that the returned values are between -50 and 50 instead of 0 and 100. I default this to true.
if sub50:
stochastic_values -= 50
CopyAll together it looks like:
@jit(nopython=True)
def stochastic(high, low, close, lookback, n_smooth, sub50=True):
"""
Build the stochastic indicator array with a specified level of smoothing.
:param high: numpy array of high prices
:param low: numpy array of low prices
:param close: numpy array of close prices
:param lookback: lookback period for the indicator
:param n_smooth: integer 0, 1, or 2 for no smoothing, one smoothing, or two smoothings
:return: numpy array of the stochastic indicator
"""
raw_k_values = np.zeros(len(close) - lookback + 1)
for i in range(lookback - 1, len(close)):
# Moving the raw_stochastic logic here
highest = np.max(high[i - lookback + 1:i + 1])
lowest = np.min(low[i - lookback + 1:i + 1])
raw_k_values[i - lookback + 1] = (close[i] - lowest) / (highest - lowest + 1.e-60) * 100.0
if n_smooth == 0:
stochastic_values = raw_k_values
elif n_smooth == 1:
stochastic_values = fast_exponential_smoothing(raw_k_values)
elif n_smooth == 2:
first_smooth = fast_exponential_smoothing(raw_k_values)
stochastic_values = fast_exponential_smoothing(first_smooth)
else:
raise ValueError("n_smooth must be 0, 1, or 2.")
if sub50:
stochastic_values -= 50
# Prepend NaNs to align with the original length
return np.concatenate((np.full(lookback - 1, np.nan), stochastic_values))
CopyVisualizations and Test Results
The generated report provides a comprehensive analysis of trading indicators, offering insights into their statistical properties, predictive power, mean stability over time, and optimal thresholds for profitability. It combines detailed statistical summaries, mutual information scores, mean break tests, and profit factor evaluations.
For these tests, I used a 14-day lookback.
Simple Statistics and Relative Entropy Report
The Simple Statistics Table summarizes key metrics for each trading indicator, including the number of cases, mean, minimum, maximum, interquartile range (IQR), range/IQR ratio, and relative entropy. In the table, a lower range/IQR ratio suggests a tighter, more predictable dataset, while an optimal relative entropy indicates a balance of diversity and uniqueness without excessive noise.
Ncases: Number of cases (bars) in feature (indicator).
Mean: Average value of the feature across all cases.
Min/Max: The minimum and maximum value of the feature across all cases.
IQR: Interquartile Range, measures range minus the top and bottom 25% of the raw range.
Range/IQR: A unitless measure of data dispersion relative to its middle 50%.
Relative Entropy: Measures the difference between two probability distributions; a value of zero indicates identical distributions.
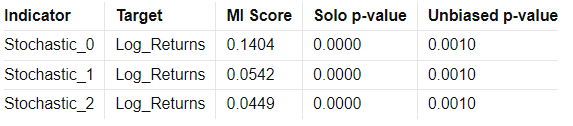
Mutual Information Report
High MI scores indicate a strong relationship between the indicator and the target variable, suggesting potential predictive power. Low p-values further validate the indicator's statistical significance.
MI Score: Measures the mutual dependence between the feature and the target.
Solo p-value: Initial significance estimate, proportion of permuted MI scores equal to or higher than the original MI scores.
Unbiased p-value: Adjusted solo p-value considering the number of permutations plus one, reducing bias.
Serial Correlated Mean Break Test Report
The Serial Correlated Mean Break Test Report identifies potential breaks in the mean of each trading indicator, taking into account serial correlation. This test helps detect significant shifts in the mean over time, indicating nonstationary behavior in the data.
nrecent: The number of recent observations considered in the test.
z(U): The greatest break encountered in the mean across the user-specified range.
Solo p-value: Measures the significance of the greatest break while accounting for the entire range of boundaries searched. If this value is not small, it suggests that the indicator does not have a significant mean break.
Unbiased p-value: Adjusted solo p-value considering the number of permutations plus one, reducing bias.
Optimal Thresholds w/ Profit Factor Report
The Optimal Thresholds w/ Profit Factor Report evaluates various threshold levels for trading indicators to identify the most profitable long and short positions. The report includes the fraction of data points greater than or equal to the threshold, the corresponding profit factor for long and short positions, and the fraction of data points less than the threshold with their respective profit factors. The optimal thresholds at the bottom indicate the threshold levels with the highest profit factors for long and short positions, while the p-values provide statistical significance for these thresholds.
Note: I need to look at the p-value calculations in the optimization reports.
Conclusion
The stochastic indicator is a simple tool with decent enough test results to consider testing in strategy development. It also serves a foundation for many other indicators. For example, you can create a Stochastic Relative Strength Indicator. I know traders who use the stochastic indicator creatively, combining it with various other indicators, and achieving some degree of success. So, it has potential to serve as a solid base for custom indicators.
Look for the update post tomorrow and a Strategy post this weekend.
Happy Hunting!
The code for strategies and the custom functions/framework I use for strategy development in Python and NinjaScript can be found at the Hunt Gather Trade GitHub. This code repository will house all code related to articles and strategy development. If there are any paid subscribers without access, please contact me via e-mail. I do my best to invite members quickly after they subscribe. That being said, please try and make sure the e-mail you use with Substack is the e-mail associated with GitHub. It is difficult to track members otherwise.
Hunt-Gather-Trade/pyquanttools
Feel free to comment below or e-mail me if you need help with anything, wish to criticize, or have thoughts on improvements. Paid subscribers can access this code and more at the private HGT GitHub repo. As always, this newsletter represents refined versions of my research notes. That means these notes are plastic. There could be mistakes or better ways to accomplish what I am trying to do. Nothing is perfect, and I always look for ways to improve my techniques.
References:
John J. Murphy. Technical Analysis of the Financial Markets. New York Institute of Finance,
Masters, T. (2013). Statistically sound indicators for financial market prediction.