Researching the Relative Strength Index in Python
We've got math, code, charts, and scatter plots in this one. It's open to all subscribers and it even comes with a PDF!
Researching the Relative Strength
This is the first post dedicated entirely to a single indicator. I will build on this post and idea as I continue to research market indicators and strategies. I am also uploading the entire research notebook as a PDF to this post. You can download and view it with the link below.
As always, the code for this notebook will be available on the GitHub repo for the paid subscribers. However, the accompanying PDF will also contain all the code, if you want to see the underlying functionality of everything that is going to be discussed here. This is the first time I decided to export my research to PDF but I hope to continue this going forward. The PDF shows the process I use when making an indicator and starting the research process. Since there is a PDF, I am going to keep most of the code out of this post. That should make it a bit more readable. For those who want to check my work, check out the PDF or clone the repo if you are a paid subscribe.
Disclaimer: the following post is an organized representation of my research and project notes. It doesn’t represent any type of advice, financial or otherwise. Its purpose is to be informative and educational. Backtest results are based on historical data, not real-time data. There is no guarantee that these hypothetical results will continue in the future. Day trading is extremely risky, and I do not suggest running any of these strategies live.
Relative Strength Index (RSI)
The Relative Strength Index (RSI) was originally introduced by J. Welles Wilder in 1978 and was designed to help remove the erratic behavior found in constructing momentum lines. [2] This is a popular tool/indicator for traders and analyst to use and is useful for helping to quantify trends. Put simply, the RSI evaluates the average size of recent increases in closing prices against decreases.
The original calculation for the RSI is: [2]
Where RS is define as: [2]
Originally, the RSI used a 14 day (period) lookback for calculations [2] and a standard moving average (SMA) for smoothing [1]. Instead of the SMA, this example will use exponential smoothing. This means that when we do bar-by-bar computations, the upward cumulation will suffer an inclusion of zero when the bar moves downwards and vice versa.
We calculate the exponential smoothing with the following equation: [1]
This equation is derived from the expression:
The RSI calculation, which is performed after each new bar is complete, looks like this:
This computation reflects the proportion of total gains versus total losses over the specified period, normalized to a 0-100 scale, making it easy to interpret relative strength or weakness in the market context. As Masters suggests, it might be beneficial to subtract 50 from final result to center the indicator at 0, especially if you are dealing with predictive models. [1]
Creating the RSI Indicator
The function we want to calculate is the Relative Strength Index (RSI) of a given set of prices, using exponential smoothing to compute the average gains and losses. It offers an option to adjust the RSI scale from the traditional range of [0, 100] to a shifted range of [-50, 50]. This adjustment can be particularly
useful in predictive modeling scenarios where a centered scale might provide clearer signals for some algorithms.
To ensure the function performs efficiently, even with the computationally intensive task of exponential smoothing, it employs Numba’s JIT (Just-In-Time) compiler. This allows the function to run at speeds suitable for intensive backtesting and real-time financial market analysis, maintaining high performance (for Python) without sacrificing the precision needed for reliable trading signals.
Logic:
Gains and Losses: For each period, calculate the difference between consecutive closing prices. Positive differences represent gains, while negative differences represent losses.
Exponential Smoothing: Apply exponential smoothing to gains and losses separately, using the ’lookback’ period as the basis for smoothing. This method prioritizes recent price movements, providing a weighted average that more accurately reflects current market conditions.
RSI Calculation: Compute the RSI using the smoothed gains and losses, converting these values into an index that ranges from 0 to 100 (or -50 to 50 if adjusted).
Note: This function utilizes the equations and methods mentioned on the first section to calculate the RSI. Comments in the code explain the purpose of each section.
Docstring:
"""
Parameters:
- close (np.ndarray): The array of closing prices.
- period (int): The number of periods to calculate the average gains and losses.
- subtract_50 (bool): If True, shifts the RSI range from [0, 100] to [-50, 50] for use in predi
Returns:
- np.ndarray: An array of RSI values where each value corresponds to the RSI
at a given point in time. The array has the same length as 'close'. RSI values
for the initial 'period' points are set to NaN because there's not enough data
to make the calculation.
Raises:
- ValueError: If 'period' is less than 1 or if 'close' array is empty.
"""
Code:
@jit(nopython=True)
def rsi(close, lookback, subtract_50=False):
n = close.size
output = np.full(n, np.nan) # Use NaN to indicate non-ready periods
# Arrays to store raw gains and losses
gains = np.zeros(n)
losses = np.zeros(n)
# Calculate gains and losses
for i in range(1, n):
delta = close[i] - close[i - 1]
if delta > 0:
gains[i] = delta
else:
losses[i] = -delta
# Arrays to store smoothed gains and losses
smoothed_gain = np.zeros(n)
smoothed_loss = np.zeros(n)
# Initialize the first values based on the first non-zero gain/loss
smoothed_gain[0] = gains[0] # Assumes the first value is an initialization step
smoothed_loss[0] = losses[0] # Same as above
# Apply the smoothing formula to gains and losses
for i in range(1, n):
smoothed_gain[i] = ((lookback - 1) * smoothed_gain[i - 1] + gains[i]) / lookback
smoothed_loss[i] = ((lookback - 1) * smoothed_loss[i - 1] + losses[i]) / lookback
# Calculate RSI
for i in range(lookback, n):
total = smoothed_gain[i] + smoothed_loss[i]
if total != 0:
rsi = 100 * (smoothed_gain[i] / total)
output[i] = rsi - 50 if subtract_50 else rsi
return output
Visualizing the RSI and interpreting results
Before plotting, I want to note a few things about the data and visualizations for reference. The data is ten years of daily data fetched using the yfinace library. The purpose of the tests at this level are to test the indicator itself and set up some simple visualizations that will help us when we get to the strategy research phase. For these purposes, the data from yfinance will be just fine. The code for this section and how I formatted my data frame can be found in the PDF.
**Addendum: Ticker used for historical data was SPY.
I will be using the Logarithmic Returns (log returns) for comparison on plots and charts. Log returns, calculated by taking the natural logarithm of the ratio of consecutive closing prices, are preferred for mathematical tractability in financial models. In the PDF, I calculate simple and cumulative returns for examples as well.
The following sections are a series of visualizations for examining the RSI and determining whether we can see any patterns or extract information manually. We will plot the RSI and returns separately and look for any apparent nonstationarity in our series. Then, we will create a series of scatter plots and get some initial impressions from our data.
RSI Plot
Impressions:
Visual inspection of the RSI plot shows our indicator (at least in the 10 year window we are looking at) is mostly stationary. Values appear to never hit the min/max values.
Log Return Plot
Impressions:
Returns appear mostly stationary. There is a clear aberrancy in 2020 that might show a break in the mean in future testing.
RSI vs. Log Returns
Impressions:
When you look at the returns above/below our threshold lines, you can see that their is a stronger correlation with returns. For example, it appears that above the upper threshold (70) there are more positive returns than there are negative.
RSI vs. Volume
Impressions:
The majority cluster is below 100,000,000 (1e8) volume. Above that value and the results are more disbursed and less tightly clustered. Further visualizations of data (RSI vs. returns) above and below this volume threshold would be ideal.
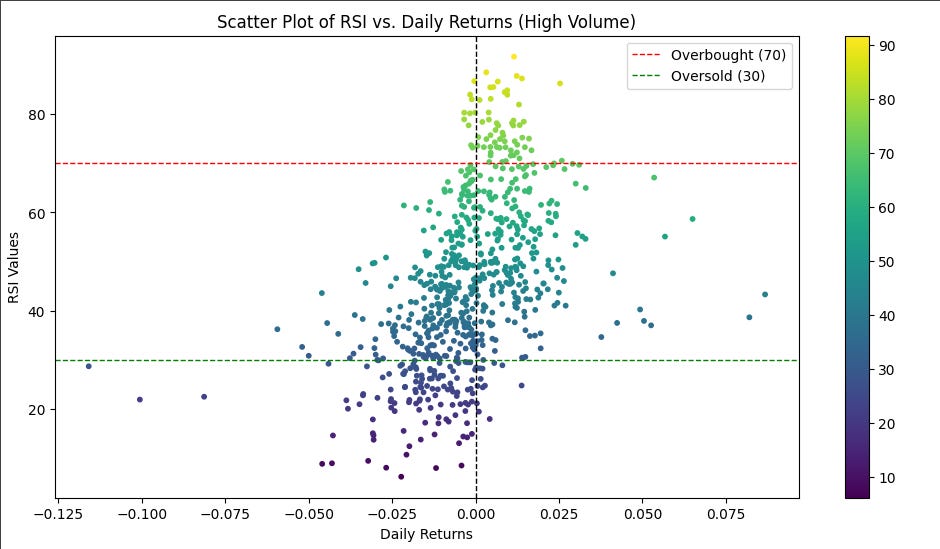
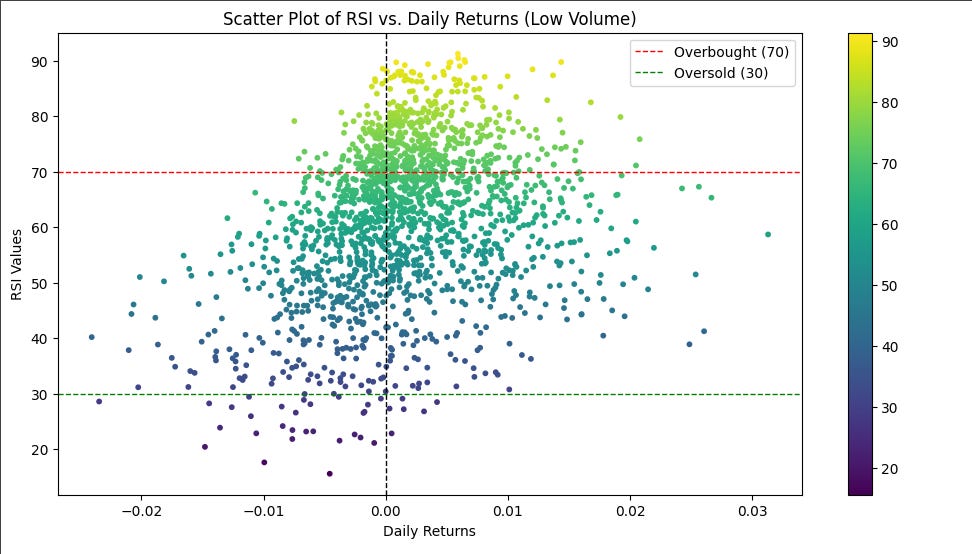
RSI vs. Log Returns w/ Volume Thresholds
Impressions:
Both plots show better returns (respectively) when we are above/below the RSI threshold values. When volume is above , the associated returns show minimal returns in the opposite direction. There seems to be a stronger correlation with negative returns when below 30 than with positive returns when above 70. However, there appear to be more observations above the top threshold than below.
Observations and Impressions
The RSI calculation functions as intended and appears to be stationary via eye test.
The scatter plot depicting the relationship between the Relative Strength Index (RSI) and returns reveals distinct patterns at the established thresholds. Notably, when the RSI exceeds the upper threshold, there is a predominant occurrence of positive returns, suggesting a strong correlation between high RSI values and upward market trends. Conversely, RSI values below the lower threshold are predominantly associated with negative returns, indicating a likely continuation of downward trends. These observations support the hypothesis that RSI values beyond these thresholds can be predictive of the corresponding trend direction in returns. This trend-predictive behavior of the RSI is particularly significant as it validates the use of RSI as a momentum indicator in technical analysis, providing insights into potential market movements based on historical price data.
The analysis of the RSI versus returns, segmented by trading volume (above and below), corroborates the initial observations that RSI extremes predict return directions. Notably, in instances where the trading volume surpasses the threshold, there are significantly fewer occurrences of returns that contradict the expected trend direction. Specifically, above the upper threshold, negative returns are less frequent, enhancing the reliability of RSI as an indicator of positive market momentum under high-volume conditions.
It is important to highlight that, despite lower volumes, the pattern of RSI aligning with directional trends in returns remains evident. This persistence suggests that while volume amplifies the predictive clarity of the RSI, the indicator itself is robust across different volume levels. This observation opens avenues for adjusting the volume threshold in future analyses to refine our understanding of volume's impact on the predictive power of the RSI.
Summary
That wasn't so bad. We have a functioning RSI indicator and some basic visualizations that might help us find an edge. The next steps would be to run the indicator through the statistical tests we created in Indicator Testing series, but first, we need to design and research the ADX and MACD indicators.
This indicator will be adapted into a Lean indicator so we can use it when we actually backtest the strategy in a couple of days. This indicator will be in the HGT repository along with everything else we cover.
Until next time, happy trading and happy coding!
The code for strategies and the custom functions/framework I use for strategy development in NinjaScript can be found at the Hunt Gather Trade GitHub. This code repository will house all code related to articles and strategy development. If there are any paid subscribers without access, please contact me via e-mail. I do my best to invite members quickly after they subscribe. That being said, please try and make sure the e-mail you use with Substack is the e-mail associated with GitHub. It is difficult to track members otherwise.
Feel free to comment below or e-mail me if you need help with anything, wish to criticize, or have thoughts on improvements. Paid subscribers can access this code and more at the private HGT GitHub repo. As always, this newsletter represents refined versions of my research notes. That means these notes are plastic. There could be mistakes or better ways to accomplish what I am trying to do. Nothing is perfect, and I always look for ways to improve my techniques.
References
[1] Timothy Masters. Statistically Sound Indicators for Financial Market Prediction. Self-Published, 2 edition, 2020.
[2] John J. Murphy. Technical Analysis of the Financial Markets. New York Institute of Finance, 1999.